Grundlagen von FloodArea¶
Anwendungsgebiete¶
FloodArea HPC 11 berechnet Überschwemmungsflächen ausgehend von:
Einem Gewässer mit vorgegebenem Wasserstand, sodass das Wasser über die Ufer tritt und sich im Umland verteilt (Hochwasser). Der Wasserstand kann räumlich (z. B. entlang eines Flusslaufes) und zeitlich variieren.
Einer Punkteinspeisung, die punktuell an Koordinaten Wasser in das Modell einspeist oder entnimmt. Die Zuflussmengen der Punkteinspeisung sind zeitlich und räumlich variabel und lassen sich auch wasserstandsabhängig definieren.
Einer Beregnung, bei der über einen größeren Bereich das Wasser zugeführt wird. Die Beregnung kann räumlich aufgeteilt werden und mit unterschiedlichen Niederschlagsganglinien durchgeführt werden. Der Abflussbeiwert des Untersuchungsgebiets kann über die Zeit der Simulation verändert werden.
Diese drei Berechnungsoptionen sind frei miteinander kombinierbar. Die Berechnungsergebnisse werden in einem vom Benutzer frei wählbaren Zeitintervall in Form von GeoTIFFs ausgegeben. Dadurch lässt sich die zeitliche Abfolge der Überflutung beliebig detailliert nachvollziehen. Die Ergebnisausgabe bzw. -darstellung erfolgt dabei je nach Wunsch in absoluten Höhenangaben oder als Überschwemmungstiefe (Höhendifferenz zur Oberfläche). Bei Bedarf können auch für jedes Zeitintervall die aktuellen Fließrichtungen und Fließgeschwindigkeiten ausgegeben werden.
Die Simulation kann durch die Angabe zusätzlicher Parameter detailliert spezifiziert werden (Optionale Funktionen). Um die Fließgeschwindigkeiten besser an die Realität anzupassen, können ergänzend Rauheitsbeiwert, kurz Rauheit, in Form eines Rasters angegeben werden. Die Rauheit kann überflutungstiefenabhängig, über einen Schalter automatisch erhöht oder verringert werden. Dies ermöglicht die realitätsnahe Abbildung des Fließverhaltens in dichter Vegetation.
Grundlagen zur Berechnungsmethode¶
Die Berechnung der Überschwemmungsbereiche basiert auf einem hydrodynamischen Ansatz.
Betrachtet werden jeweils die 8 Nachbarn einer Rasterzelle. Das Abflussvolumen zu den Nachbarn wird mit Hilfe der Fließformel nach Manning-Strickler errechnet:
dabei ist \(r_{hy}^{\frac{2}{3}}\) der hydraulische Radius und \(I^{\frac{1}{2}}\) das Gefälle.
Für die \(k_{St}\) -Werte (Rauheit) liegen ausführliche Tabellenwerke vor, was ein deutlicher Vorteil dieser Fließformel gegenüber vergleichbaren ist. Da die Rauheit linear in die Fließgeschwindigkeit ( \(V\) ) eingeht, ist eine möglichst gute Abschätzung für die Qualität der Simulationsergebnisse entscheidend.
Die Fließtiefe ergibt sich jeweils aus der Differenz zwischen dem Wasserspiegel und der maximalen Geländehöhe entlang der Fließstrecke im entsprechenden Iterationsintervall:
In jedem Iterationsschritt wird die Neigung des Wasserspiegels neu berechnet und die Wasserspiegellinie in Richtung der größten Neigung für die Gefälleangabe in der Manning-Strickler-Formel verwendet.
Bemerkung
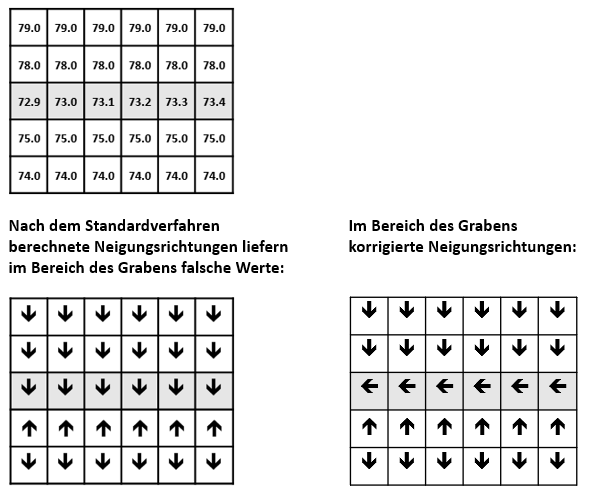
Diese Berechnung von Neigung und Exposition kann in Sonderfällen versagen. Im Fall von 1 Pixel breiten linearen Elementen kann die Neigung teilweise quer zum Graben ausgegeben werden, wenn die Grabensohle geringer geneigt ist als die Umgebung. Um solche Anmerkung zu vermeiden, wird das Ergebnis auf Plausibilität überprüft, indem der Höhenwert der jeweiligen Zentralrasterzelle mit der in Neigungsrichtung gelegenen verglichen wird. Weist die Zelle in Neigungsrichtung größere Höhenwerte auf, wird der niedrigste Wert aus der 8-Nachbar-Umgebung gesucht und die Neigung direkt aus der Höhendifferenz abgeleitet.
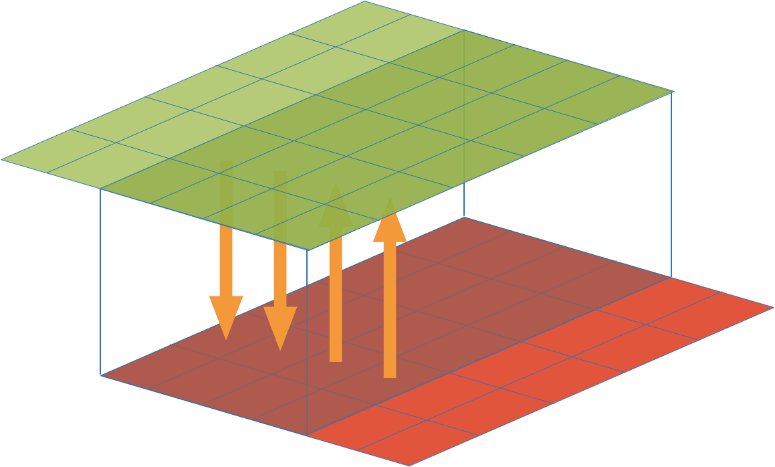
Das folgende Beispiel zeigt Höhenwerte eines exemplarischen Originalhöhenmodells mit einem Graben. Die Neigung des Grabens ist hier geringer als die Neigung des Geländes (Bild unten).
Die errechnete Fließgeschwindigkeit wird mit dem Fließquerschnitt und dem Iterationsintervall multipliziert und ergibt die Austauschmenge für den aktuellen Rechenschritt. Da die Fließformel nach Manning-Strickler nur für Normalabfluss gültig ist (d. h. Reibungsverlust gleich dem Gewinn an Lageenergie) werden außerhalb des Gültigkeitsbereiches (z. B. bei Beschleunigung) teilweise zu hohe Fließgeschwindigkeiten berechnet. Daher werden die errechneten Fließgeschwindigkeiten dahingehend überprüft, ob sie das Grenzkriterium
\(V = \sqrt{g \cdot h}\) (Ausbreitungsgeschwindigkeit von Störwellen)
erfüllen. Zu hohe Geschwindigkeiten werden entsprechend reduziert.
Mit den Volumen werden zugleich die Geschwindigkeitsvektoren übergeben. Diese werden addiert und als Grundgeschwindigkeit für das folgende Iterationsintervall zugrunde gelegt. Zur Bestimmung der jeweiligen Fließgeschwindigkeit wird das arithmetische Mittel aus der aktuellen Geschwindigkeitsberechnung und dem Ergebnis der Vektoraddition gebildet. Durch diese Geschwindigkeitsübertragung werden plötzliche Fließwechsel- bzw. Fließumkehrprozesse minimiert und Trägheitseffekte vereinfachend nachgebildet.
Rechenperformance¶
FloodArea HPC 11 ist parallelisiert – das Gebiet wird während der Simulation in Kacheln aufgeteilt (Tiling) und die Kacheln werden auf die Prozessor-Kerne des Rechencomputers verteilt.
Die Kacheln überlappen sich an den Rändern um 4 Pixel, um den simulierten Abfluss an den Rändern der Kacheln zu synchronisieren. Bei älteren Versionen haben sich die Kacheln nur um 3 Pixel überlappt - die Erhöhung der Pixel hat zur Verbesserung der Synchronisation und höherer Genauigkeit der Volumenbilanz geführt. Die Aufteilung des Gebiets auf die Rechenkerne führt zu einer optimalen Nutzung der Rechenleistung, unabhängig von der Anzahl an Kernen.
Das Preprocessing der Eingangsdaten, das bisher seperat über Python-Scripts lief, wurde in C++ in den Core inkludiert. Der Rechenstart wurde somit deutlich vereinfacht und zeitlich verkürzt. Die Simulationszeit hängt von der individuellen Hardware ab, aber bei Tests auf unterschiedlichen Computern wurden Verkürzungen der Rechenzeiten um den Faktor 2 bis 3 im Vergleich zu FloodArea HPC 10.3 festgestellt.
Bei Tests im Rahmen eines universitären Forschungsprojekts wurden Geschwindigkeitszunahmen von bis zu einem Faktor von 4 erreicht. FloodArea HPC 11 weist zudem eine höhere Stabilität der Rechenzeit gegenüber der Größe und insbesondere der Form des Simulationsgebiets (Anteil an NoData, Passform der Kacheln etc.) auf, als FloodArea HPC 10.3.
Einschränkungen¶
Volumenbilanz bei geringen Wassermengen¶
Es ist zu beachten, dass FloodArea für Wassermengen wie bei Flussüberschwemmungen oder Starkregen ausgelegt ist. Strömungsprozesse beginnen (real und im Modell) erst ab wenigen 1/10 Millimeter. FloodArea rechnet intern mit Werten von 1/100 mm. Wassermengen ab 0.02 mm werden in die Ausgabe geschrieben. Frühere Versionen von FloodArea hatten einen Schwellenwert von 1 mm. Dies bedeutet, dass der Wasserhaushalt nicht für Niederschläge unterhalb des Benetzungsverlustes geeignet ist und Volumenverluste bei geringen Niederschlagsmengen, werden mit größeren Niederschlagsmengen relativ kleiner. Bei normalen Starkregenereignissen beträgt der Volumenverlust maximal 1-2%.
Betrachtung von Randbereichen¶
Die Betrachtung der Randbereiche des Simulationsgebietes kann zu Problemen führen, da über den Bereich jenseits des untersuchten Gebiets keine Informationen vorhanden sind. FloodArea HPC 11 geht hier von einem Fließhindernis aus, wodurch es zu einer unrealistischen Aufstauung der Abflussvolumina am Rand des Geländemodells kommen kann.
Gerinnehydraulik¶
Das vorliegende Werkzeug ist in erster Linie zur Errechnung von Überschwemmungsbereichen gedacht. Es ist ein vereinfachtes 2-dimensionales hydraulisches Modell. Die Vereinfachungen wirken sich vor allem im Bereich der Gerinnehydraulik aus. Zum einen führt die meist verhältnismäßig grobe Auflösung des Geländemodells im Gerinnebereich zu Ungenauigkeiten. Zum anderen bedingt die fehlende Impulsübertragung zu gewissen Einschränkungen in der Aussagefähigkeit. So wird beispielsweise die Schräglage des Wasserspiegels in Flussbiegungen nicht exakt abgebildet.